小学生需要上思维训练课么,创新思维训练小学数学思维能力训练
数学思维能力的养成不是一蹴而就的,而是需要长期的练习。小达老师整理了一些数学思维能力训练题目,每日陪孩子一起做做题,不仅能加强亲子关系,还能活活脑哦~
数学思维能力训练题
1、喜羊羊星期天去买了10个苹果,它第一天吃2个,第二天吃4个,第三天吃了多少它给忘记了。最后还剩下3个苹果没有吃。请问喜羊羊第三天吃了多少个苹果?
2、小刚在超市买了两件衣服,两条裤子.请帮小刚算一算,有( )种不同的穿法。
3、三个小组共有180人,一、二两个小组人数之和比第三小组多20人,第一小组比第二小组少2人,求第一小组的人数。
4、一杯牛奶,小明第一次喝了一半,用水添满,第二次他又喝了一半,再用水添满,第三次他全部喝光。问:小明前后一共喝了多少杯水?
5、全家四口人,父亲比母亲大3岁,姐姐比弟弟大2岁。4年前他们全家的年龄之和是58岁,而现在是73岁。问现在母亲的年龄是多少岁?
6、比赛用的足球是由黑、白两色皮子缝制的,其中黑色皮子为正五边形,白色皮子为正六边形,并且黑色正五边形与白色正六边形的边长相等。缝制的方法是:每块黑色皮子的5条边分别与5块白色皮子的边缝在一起;每块白色皮子的6条边中,有3条边与黑色皮子的边缝在一起,另3条边则与其他白色皮子的边缝在一起。如果一个足球表面上共有12块黑色正五边形皮子,那么,这个足球应有白色正六边形皮子多少块?
7. 有七个排成一列的数,它们的平均数是 30,前三个数的平均数是28,后五个数的平均数是33。求第三个数。
8. 有两组数,第一组9个数的和是63,第二组的平均数是11,两个组中所有数的平均数是8。问:第二组有多少个数?
9.小明参加了六次测验,第三、第四次的平均分比前两次的平均分多2分,比后两次的平均分少2分。如果后三次平均分比前三次平均分多3分,那么第四次比第三次多得几分?
10. 乙、丙两数的平均数与甲数之比是13∶7,求甲、乙、丙三数的平均数与甲数之比。
11. 甲、乙两班进行越野行军比赛,甲班以4.5千米/时的速度走了路程的一半,又以5.5千米/时的速度走完了另一半;乙班在比赛过程中,一半时间以4.5千米/时的速度行进,另一半时间以5.5千米/时的速度行进。问:甲、乙两班谁将获胜?
12. 轮船从A城到B城需行3天,而从B城到A城需行4天。从A城放一个无动力的木筏,它漂到B城需多少天?
13. 小红和小强同时从家里出发相向而行。小红每分走52米,小强每分走70米,二人在途中的A处相遇。若小红提前4分出发,且速度不变,小强每分走90米,则两人仍在A处相遇。小红和小强两人的家相距多少米?
14. 小明和小军分别从甲、乙两地同时出发,相向而行。若两人按原定速度前进,则4时相遇;若两人各自都比原定速度多1千米/时,则3时相遇。甲、乙两地相距多少千米?
15. 甲、乙两人沿400米环形跑道练习跑步,两人同时从跑道的同一地点向相反方向跑去。相遇后甲比原来速度增加2米/秒,乙比原来速度减少2米/秒,结果都用24秒同时回到原地。求甲原来的速度。
16. 甲、乙两车分别沿公路从A,B两站同时相向而行,已知甲车的速度是乙车的1.5倍,甲、乙两车到达途中C站的时刻分别为5:00和16:00,两车相遇是什么时刻?
17. 一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长是385米。坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是多少秒?
18. 在一条马路上,小明骑车与小光同向而行,小明骑车速度是小光速度的3倍,每隔10分有一辆公共汽车超过小光,每隔20分有一辆公共汽车超过小明。已知公共汽车从始发站每次间隔同样的时间发一辆车,问:相邻两车间隔几分?
19. 一只野兔逃出80步后猎狗才追它,野兔跑 8步的路程猎狗只需跑3步,猎狗跑4步的时间兔子能跑9步。猎狗至少要跑多少步才能追上野兔?
20. 甲、乙两人在铁路旁边以同样的速度沿铁路方向相向而行,恰好有一列火车开来,整个火车经过甲身边用了18秒,2分后又用15秒从乙身边开过。问: (1)火车速度是甲的速度的几倍? (2)火车经过乙身边后,甲、乙二人还需要多少时间才能相遇?
21.小松读一本书,已读与未读的页数之比是3∶4,后来又读了33页,已读与未读的页数之比变为5∶3。这本书共有多少页?
22. 有一批待加工的零件,甲单独做需4天,乙单独做需5天,如果两人合作,那么完成任务时甲比乙多做了20个零件。这批零件共有多少个?
23. 完成一件工作,需要甲干5天、乙干6天,或者甲干 7天、乙干2天。问:甲、乙单独干这件工作各需多少天?
24.一个分数的分子与分母的和是23,分母增加19后得到一个新的分数,把这个新分数化为最简分数是1/5,求原来的分数。
参考答案
1、1个
【解析】10-2-4-3=1(个)
2、有4种不同的穿法
【解析】选择衣服的情况有2种,选择裤子的可能性有2种。选择一件衣服,一条裤子的可能性有2×2=4(种)
3、第一小组的人数49人
【解析】先将一、二两个小组作为一个整体,这样就可以利用基本和差问题公式(和+差)÷2=大数,得出第一、二两个小组的人数和(180+20)÷2=100(人),然后对第一、二两个组再作一次和差基本问题计算公式(和-差)÷2=小数,就可以得出第一小组的人数(100-2)÷2=49人。
4、小明前后一共喝了一杯水
【解析】一共喝了一杯水。一共添了两次水,每次半杯,添了共一杯水。全部喝完,即喝了一杯水。
5、现在母亲的年龄是31岁
【解析】四年前每人都应该减少4岁,全家的年龄和就应该减去4×4=16岁。但是73-58=15岁,说明4年前弟弟还没有出生。所以弟弟的年龄就是15-12=3岁,姐姐的年龄就是3+2=5岁。父母年龄和就是73-3-5=65岁。由于父母年龄差是3岁,利用和差公式,可求出母亲年龄就是(65-3)÷2=31岁。
6、这个足球应有白色正六边形皮子20块
【解析】①一个足球表面上共有12块黑色正五边形皮子,所以黑色皮子的总边数是5×12=60(条)
②每块白色皮子的6条边中,有3条边与黑色皮子的边缝在一起,另3条边则与其他白色皮子的边缝在一起,说明白色皮子的总边数是黑色皮子的两倍,所以白色皮子的总边数是60×2=120(条)
③白色皮子是正六边形,所以它的块数有120÷6=20(块)
7、39
【解析】28×3+33×5-30×7=39。
8、x=3
【解析】设第二组有x个数,则63+11x=8×(9+x),解得x=3。
9、1
【解析】第三、四次的成绩和比前两次的成绩和多4分,比后两次的成绩和少4分,推知后两次的成绩和比前两次的成绩和多8分。因为后三次的成绩和比前三次的成绩和多9分,所以第四次比第三次多9-8=1(分)。
10、11:7
【解析】以甲数为7份,则乙、丙两数共13×2=26(份) 所以甲乙丙的平均数是(26+7)/3=11(份) 因此甲乙丙三数的平均数与甲数之比是11:7。
11、乙班获胜
【解析】 快速行走的路程越长,所用时间越短。甲班快、慢速行走的路程相同,乙班快速行走的路程比慢速行走的路程长,所以乙班获胜。
12、24天
【解析】轮船顺流用3天,逆流用4天,说明轮船在静水中行4-3=1(天),等于水流3+4=7(天),即船速是流速的7倍。所以轮船顺流行3天的路程等于水流3+3×7=24(天)的路程,即木筏从A城漂到B城需24天。
13、2196米
【解析】 因为小红的速度不变,相遇地点不变,所以小红两次从出发到相遇的时间相同。也就是说,小强第二次比第一次少走4分。由 (70×4)÷(90-70)=14(分) 可知,小强第二次走了14分,推知第一次走了18分,两人的家相距 (52+70)×18=2196(米)。
14、24km
【解析】 每时多走1千米,两人3时共多走6千米,这6千米相当于两人按原定速度1时走的距离。所以甲、乙两地相距6×4=24(千米)
15、x=7又1/3米
【解析】因为相遇前后甲、乙两人的速度和不变,相遇后两人合跑一圈用24秒,所以相遇前两人合跑一圈也用24秒,即24秒时两人相遇。 设甲原来每秒跑x米,则相遇后每秒跑(x+2)米。因为甲在相遇前后各跑了24秒,共跑400米,所以有24x+24(x+2)=400,解得x=7又1/3米。
16、9∶24。
【解析】甲车到达C站时,乙车还需16-5=11(时)才能到达C站。乙车行11时的路程,两车相遇需11÷(1+1.5)=4.4(时)=4时24分,所以相遇时刻是9∶24。
17、11
【解析】快车上的人看见慢车的速度与慢车上的人看见快车的速度相同,所以两车的车长比等于两车经过对方的时间比,故所求时间为11 。
18、8分
【解析】设车速为a,小光的速度为b,则小明骑车的速度为3b。根据追及问题“追及时间×速度差=追及距离”,可列方程 10(a-b)=20(a-3b), 解得a=5b,即车速是小光速度的5倍。小光走10分相当于车行2分,由每隔10分有一辆车超过小光知,每隔8分发一辆车。
19、192
【解析】狗跑12步的路程等于兔跑32步的路程,狗跑12步的时间等于兔跑27步的时间。所以兔每跑27步,狗追上5步(兔步),狗要追上80步(兔步)需跑[27×(80÷5)+80]÷8×3=192(步)。
20、675
【解析】(1)设火车速度为a米/秒,行人速度为b米/秒,则由火车的 是行人速度的11倍; (2)从车尾经过甲到车尾经过乙,火车走了135秒,此段路程一人走需1350×11=1485(秒),因为甲已经走了135秒,所以剩下的路程两人走还需(1485-135)÷2=675(秒)。
21、168页
【解析】开始读了3/7 后来总共读了5/8 33/(5/8-3/7)=33/(11/56)=56*3=168页
22、180个
【解析】 甲和乙的工作时间比为4:5,所以工作效率比是5:4 工作量的比也5:4,把甲做的看作5份,乙做的看作4份 那么甲比乙多1份,就是20个。因此9份就是180个 所以这批零件共180个 .
23、16天
【解析】甲需要(7*3-5)/2=8(天) 乙需要(6*7-2*5)/2=16(天)
24、7/16
【解析】新分数分子与分母的和是23+19=42,化为最简分数后,分子与分母的和是1+5=6,说明1/5是用42÷6=7约分得到的,那么,没有约分时的新分数的分子是1×7=7,分母是5×7=35,原来的分母是35-19=16,原来的分数就是7/16。
小学数学思维课有必要学吗,这个训练让孩子突破思维的天花板,在家就能学



小学生数学思维训练,日本“国宝级”数学启蒙教材-百花思维训练法pdf+指导手册+视频


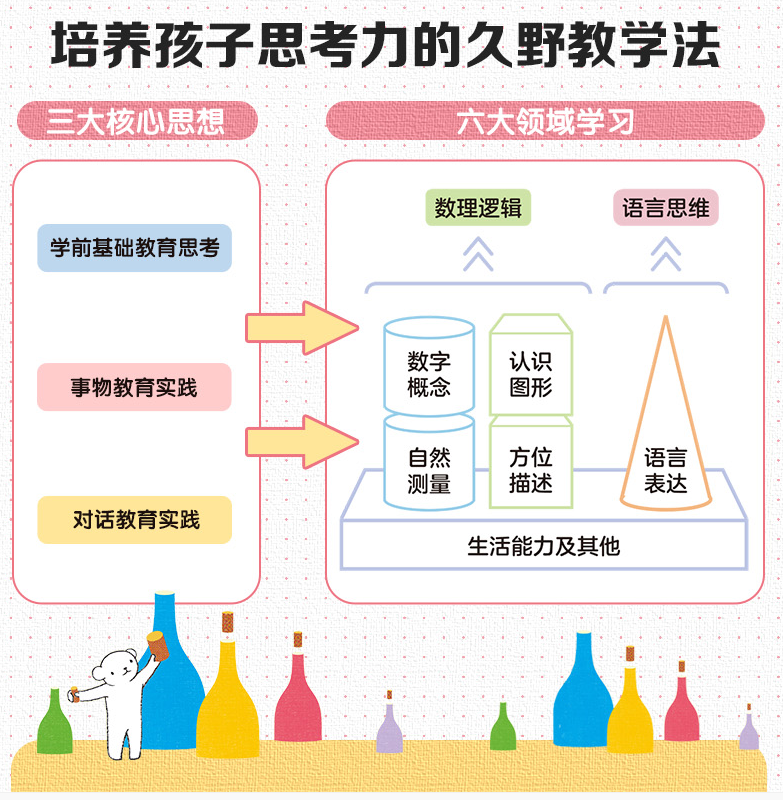
小学生思维导图课程,培养宝宝的逻辑思维,日常渗透式方法,零散时间就可以玩



精选推荐
- [记忆方法] 最有效的备考方法,法考如何备考,2021年高考备考:8种高效记忆方法
- [记忆方法] 考前快速大量记忆技巧,最有效的备考方法,考前冲刺:一消备考也要动脑筋,这样记忆方法大多数考生并不知道
- [记忆方法] 怎样快速记忆知识点且记得牢,考前快速大量记忆技巧,会计从业备考不放假,六大归纳记忆法带你飞!
- [记忆方法] 快速记忆方法的小窍门,怎样快速记忆知识点且记得牢,这些记忆方法让你学习、备考的效率大大提升!
- [精品记忆课] 记忆课程有没有效果,记忆力课程,“超强记忆”吸引家长买了课,没上几节校长就失联,41名家长能要回16万余元的培训费用吗?
- [精品记忆课] 最强大脑记忆训练法视频,记忆课程有没有效果,超强记忆系统课_第2节 底层逻辑篇 超强记忆系统课_第2节
- [古诗词记忆] 孩子记忆力差,背书困难怎么办,有什么快速背书的方法,有用的背书方法,快收藏码住吧~
- [记忆方法] 记忆的方法和技巧,记忆宫殿训练方法,技巧:熟记这些顺口溜,轻松记忆历史朝代知识
- [记忆方法] 历史朝代记忆口诀,记忆的方法和技巧,我国历史朝代顺序记忆口诀
- [古诗词记忆] 文科怎么背怎样才能记得住,文科背书怎么背得快又牢固,文科成绩难提高?你需要这12个方法