常见的九种二次曲面方程，吴帆博士译作：直线与曲面

由于日常生活中俯拾皆是，曲面的概念对我们来说是熟悉的。放眼四周，桌面、弹珠、罐头盒子，这些都是我们会即刻与“曲面”这一名称联系起来的事物。然而从数学观点看来，这些只不过是名为“曲面”的理想对象的近似物。想象桌面的厚度为零并且朝所有方向无限延展，这就得到了一个平面；掏空弹珠，只留下它与空气接触的外表面，并且假定这个表面完全光滑，这就得到了一个球面；对罐头盒子施以同样操作，并且去掉盖子和底面，这就得到了一个圆柱面。

图1：从左到右依次是圆锥面模型、（放在立方体上的）球面模型与圆柱面模型。这些曲面都放在一个平面上。

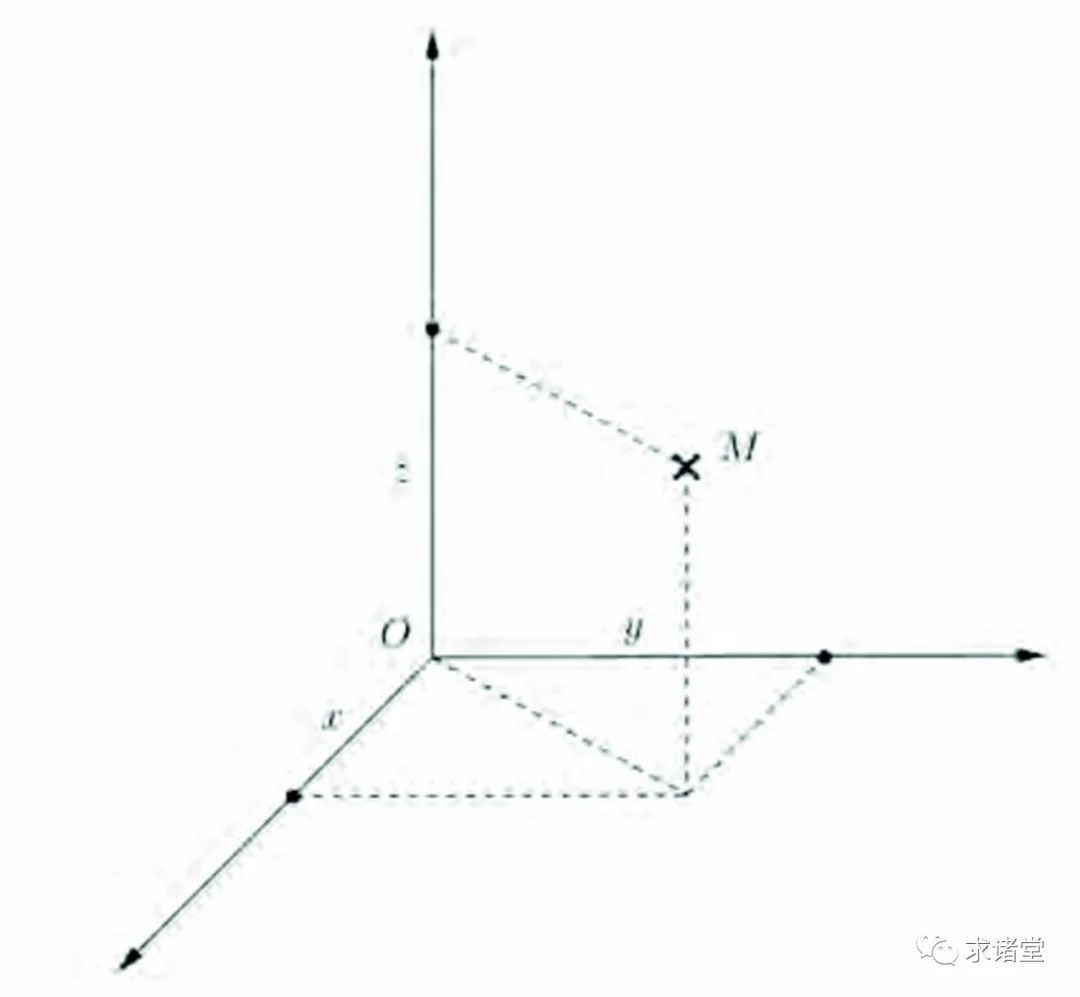
研究这些曲面有个非常实用的方法，就是使用空间坐标。 原理是：选定一个点（称为原点），取定由此点出发的三根轴，然后就可以如下图2所示，给空间中每个点 M 配以唯一的一组坐标 。

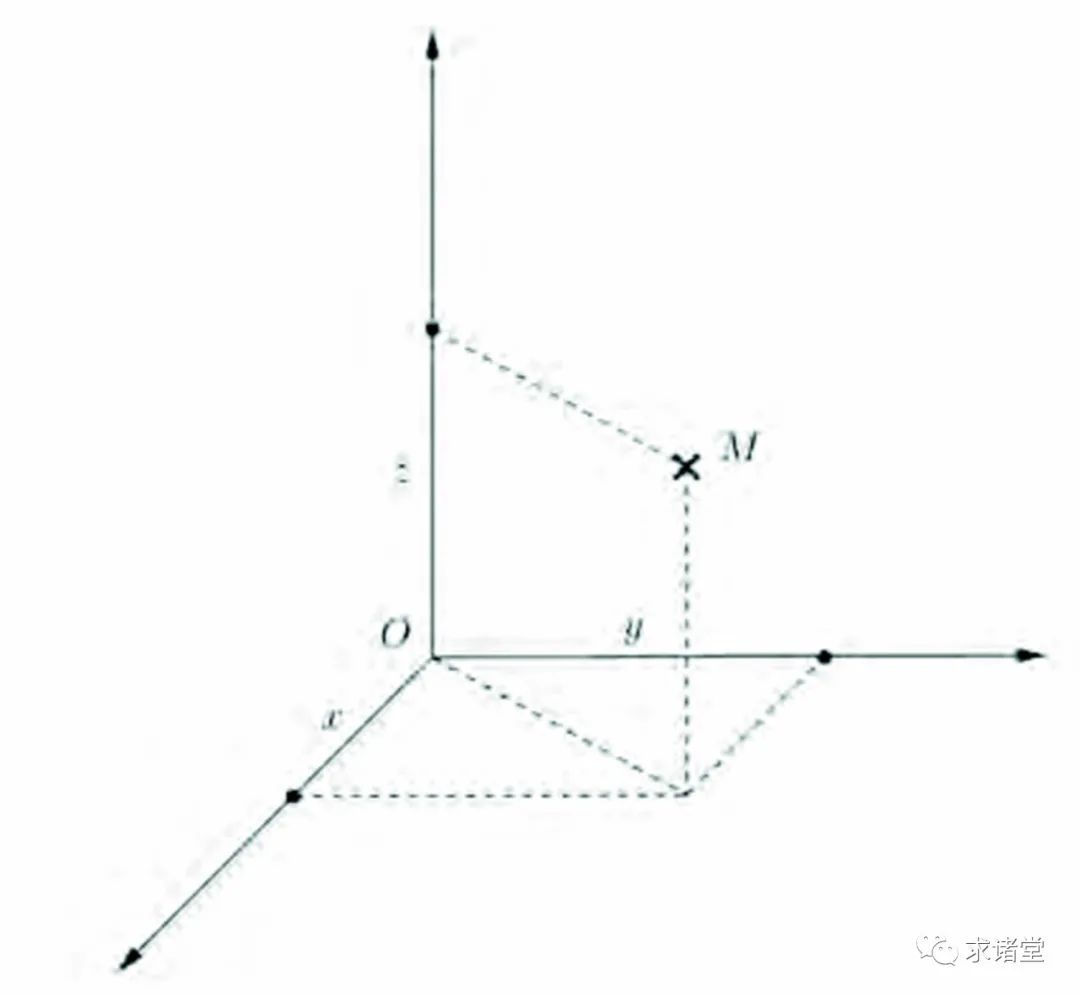
图2：具有坐标的点。字母, 与 分别表示从原点到每个用黑色圆圈标记的点之间的距离。

装备上这样的坐标之后，空间中的曲面就可以用方程来描写。例如，可以证明平面可以由只包含坐标之和或差（可能乘以倍数）的方程来定义，就是像 这样的方程；这就是说组成这个平面的点的坐标 都满足等式 。如此，由于 ，所以坐标为 的点在这个平面上；由于 ，所以坐标为 的点不在这个平面上。类似地，我们可以证明以原点为球心以1为半径的球面可以用方程 来表示。

从在身边观察到的相对简单的曲面出发，我们给出了这些曲面的方程。 不过也可以提出反向的问题，就是预先任选一个方程，然后尝试研究由其定义的曲面的性质：它长得像什么？ 是光滑还是有尖点？ 是否有洞？ 是不是有界限？

在二次曲面的情形，数学家们回答这些问题已有几个世纪之久。 二次曲面的定义方程，一方面要求 之间只能使用加、减、乘、乘方这些运算（也就是说禁止考虑例如对数或余弦这类运算），另一方面要求每一项的次数不得超过 。 因此方程

定义了三张二次曲面。 如前所见，第一个方程是球面的方程。 第二个与第三个分别是圆锥面与单叶双曲面的方程——最后这张曲面长得就像，比方说，核电站的冷却塔。

图3：单叶双曲面模型

如图3与图4所示，圆锥面、圆柱面与单叶双曲面有个共同的性质： 每张曲面都可以分解为一族直线 。换言之，这些曲面是无数条排列巧妙的直线的集合。由于这条性质，这类曲面被称为“直纹面”。

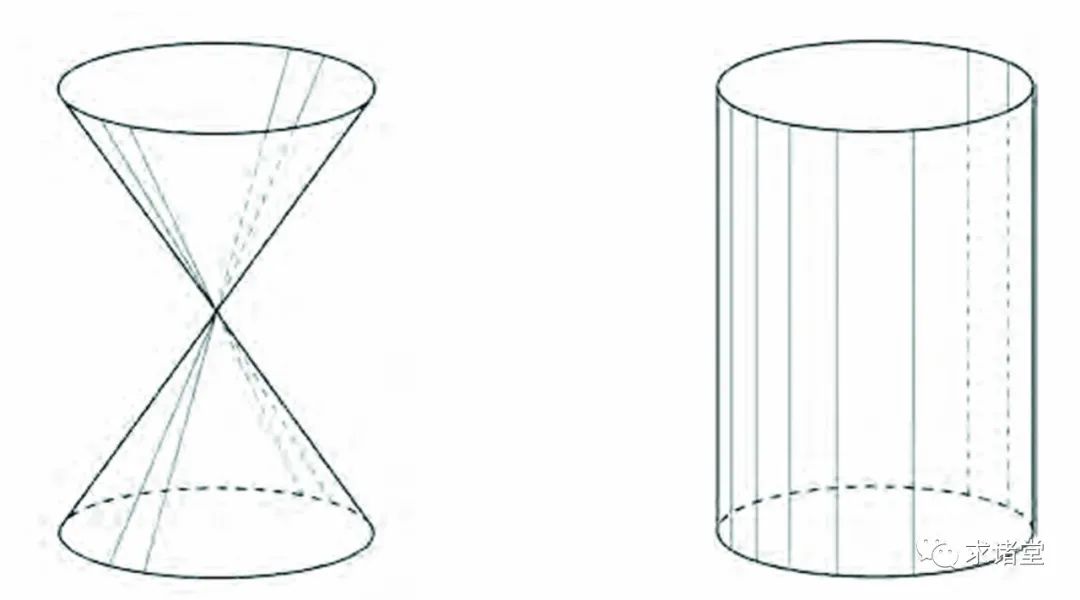
图4：圆锥面与圆柱面都是直纹面：前者由过顶点的一族直线构成，后者由与一个圆垂直相交的一族直线构成。

相反，回过头来考虑球面，就会发现一切都让人感到它不可能是直纹面：甚至都看不出来一条直线如何能够嵌入球面！事实上，有一种数学观点可以确保球面是直纹面。这个观点的（其中一条）要求是允许不仅考虑坐标为实数的点，而且也要考虑坐标为复数的点。于是方程 所表示的球面，不仅包含实数坐标为 的点，也包含复数坐标为 的点，其中 就是著名的虚数，满足 。一旦采纳这种观点，我们就可以证明球面是直纹面，进一步有所有二次曲面都是直纹面！如是，采用复坐标可以使我们得到更一般的结果，但要付出一点代价：具有复坐标的点不再能够如我们习惯的那样画出来了。我们通常采用的球面图示就变得不完整了（因为它只能展现实坐标的点），球面上包含的直线就更不可能表现出来了……

现在来谈谈三次曲面，也即这些曲面定义方程中项的次数不超过3，例如

历史上对这类曲面的研究比较晚近，19世纪中叶才开始。与之相对，二次曲面从古希腊时代以来就是研究对象：特别是， 阿基米德（公元前3世纪）就已经明了如何计算球、圆柱与圆锥的表面积与体积。对三次曲面的早期研究有着重大贡献的数学家之一是Arthur Cayley (1821-1895)。他研究了一类直纹三次曲面，图5展示了这种曲面的一个模型。

图5：一个直纹三次曲面的线材模型

与二次曲面不同，三次曲面不全是直纹的（哪怕使用了复坐标）。事实上，除了例外情形，三次曲面只包含有限多条直线。还有更好的结论：（几乎所有）三次曲面都包含同样数目的直线，即27条。然而应该留意这一事实：仅当使用复坐标时这一结论才是对的。也就是说，有时这27条直线中有若干条不能在模型上具体表现出来（见图6）。（几乎所有）三次曲面上存在27条直线的定理是1849年在Cayley与同事George Salmon的书信往来中证明的（注1）。

注1：另一方面，如果曲面的定义方程中有一项的次数大于等于4，那么这个曲面上一般不会包含任何直线。

图6：左边的曲面模型上标出了27条直线，而右边的曲面模型上仅能标出7条，另外20条是由复坐标的点组成的。

例外情形一方面是直纹三次曲面（包含无穷多条直线），另一方面是带奇点的三次曲面，这些曲面有尖点或者挤压的形状（如图7中两个模型上的特殊部位）。 这后一类三次曲面仍然包含有限多条直线，只是少于27条。

图7：两个带奇点的三次曲面模型。底下这个是Cayley曲面。

27条直线的定理受到了19世纪一些数学家的热烈欢迎。例如James Joseph Sylvester在1869年写道：

★

阿基米德将圆柱、圆锥与球面刻在他的墓碑上，我们出色的同胞也能以同样正当的理由立下遗嘱，将带27根直线的三次曲面（译注：Sylvester此处特地造了一个词cubic eikosiheptagram）刻在他们的墓碑上。宇宙之灵！我们将去往何处？所有这一切将在何时何处如何结束？

”

但三次曲面的早期研究，包括27条直线的存在性的证明，仍然十分抽象，于是接下来就提出了关于曲面形状及其上27条直线的配列方式的问题。 Sylvester已于1861年通过有机的比喻表达了建造这一构型的铁丝模型的意愿：

想用铁丝或者黄铜丝搭建这27条直线的系统 [...]，这样我们就可以用肉眼看到[三次]曲面上的所有直线（可以说是骨骼），体验到出乎意料的乐趣。

看来Sylvester本人之后未能实现这样的模型，但其他数学家（包括Cayley）对这个问题发生了兴趣并开展了研究，旨在为具体构造提供充分的数值信息： 这些数值一方面要足够精确，使得制成的形状能够忠实于现实，另一方面又要确保全部27条直线可以在合理的空间范围内都表示出来。

在本文结束之际，我们还要提到德国数学家Alfred Clebsch (1833 - 1872)的名字，他对几何学，尤其在三次曲面这一主题上做出了重大贡献。 对于Clebsch而言，几何直观在数学中起着本质作用，因此模型对于深入理解曲面来说是极其重要的。 Clebsch也常常寻求将几何观点引入那些看上去远离几何的数学领域。于是在与代数方程论（旨在理解一元方程的性质的代数分支） 相关的研究中他发现了一类比较特别的三次曲面，他称之为“对角曲面”。 在他身后这类曲面被重新命名为“Clebsch曲面”或者“Clebsch对角曲面”。

图8：Clebsch对角曲面的不同模型

1872年Clebsch制成了一个带27条直线的对角曲面的石膏模型，在哥廷根科学院的一次集会上他披露并描述了这一模型。 这个模型尔后成了众多三次曲面模型的标志。 例如，那个时代伟大的德国数学家、Clebsch的学生Felix Klein (1849-1925)把这个模型带到1893年芝加哥万国博览会上展出。 如今人们可以在世界各地的多处藏品中找到Clebsch对角曲面模型。 特别是在亨利庞加莱研究所的收藏中有一系列45个三次曲面的模型，相应于三次曲面45种可能的形状。

【注】本文译自亨利庞加莱研究所编著的Objets mathématiques一书中的篇目Des droites et des surfaces，作者是数学史家 François Lê。