排序记忆法举例，从肌肉记忆到《几何原本》第四公理 - 第四届数学文化征文

本文为“2022年第四届数学文化征文活动

从肌肉记忆到《几何原本》第四公理

作者 : 蒲定东

作品编号：069

（檀小七巧板社团课，一年级同学在图证剖分相等，对应《几何原本》第二公理——等量加等量，其和相等）

从2020年秋季开学至今，檀木林小学七巧板社团主要面向一、二年级学生招新，而之前只招过五年级学生。孩子们对拼图游戏的兴趣是与生俱来的，大人们则希望有些许引导，让孩子们觉得数学好玩。

作为社团指导老师，在语言方面，我只能将数学概念、术语转换为孩子们生活中的熟悉的自然语言来表达。例如，全等拼图，我说成双胞胎拼图。

更进一步，引导孩子们植根于肌肉记忆去发现。因为，孩子是用肢体去探索世界的，孩子的肢体是探索的主角，孩子的肢体不是孩子大脑的奴隶。孩子的大脑尚未受到语言的污染。

例如，关于全等，我这样导入：

同学们有没有发现，有的大人的左手和右手不一样大。你怎样证明，你的左手跟右手是一样大的？或者不一样大？

这时候，大多数孩子会下意识地双手合十，仔细检视，然后踊跃反馈自己的发明与发现。

这时候，我会趁热打铁，赞叹孩子们独立发现、重新发现了《几何原本》第四公理——彼此重合（的东西）彼此相等。并让孩子们写下来，贴到家里书房的墙上。

对于孩子，先是从生活到数学，后是从数学到生活。我们需要去挖掘植根于肌肉记忆的第四公理这样的桥梁，连接起生活与数学。

（一）

关于旋转的语言，孩子们没接触过角度，我就用钟点来表达。例如，从12点走到3点，用以表达顺时针旋转90度。

旋转与翻转植根于肌肉记忆。平移或许处于更底层。旋转并且平移呈现为滚动，那么，旋转中心是禁止平移的，是不动的。同理，翻转中轴也是禁止平移的，是不动的。动手操作更能体会。

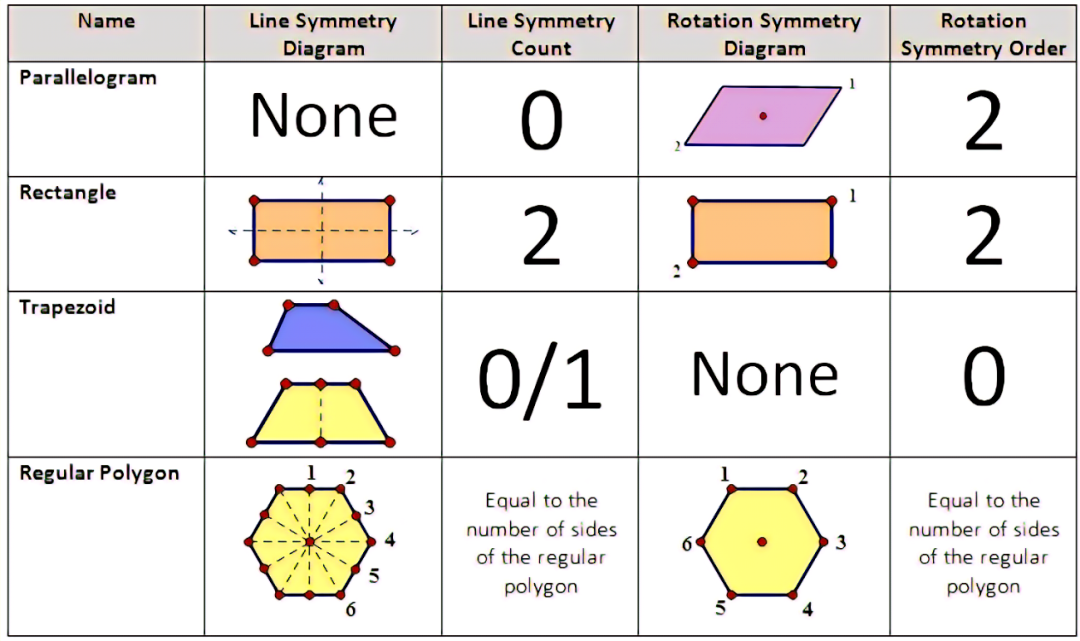
若一个拼块，经过一次旋转变换，从起点出发又回到起点，终点与起点彼此重合彼此相等，我们就说该拼块构成一种旋转对称。

例如，平行四边形拼块有两种旋转对称，从3点钟旋转到9点钟，彼此重合彼此相等；再从9点钟旋转到3点钟彼此重合彼此相等。

正方形拼块有四种旋转对称。自己去发现。

更深层次的问题来了，三角形拼块自身是否具备旋转对称？我答不上来，但能提问题，或许蕴含着思考者超越的契机。

若一个拼块，经过一次翻转变换，从起点出发又回到起点，终点与起点彼此重合彼此相等，我们就说该拼块构成一种翻转对称。

在对折的意义上，三角形拼图构成一种翻转对称，对称轴只有一条。正方形拼图具备四种翻转对称，对称轴有四条。

我的疑惑是，三角形拼块，从正面翻转到反面，彼此重合彼此相等；再从反面翻转到正面，彼此重合彼此相等，是不是意味着它具备两种翻转对称呢？

（二）

我总是惊叹于小孩子很自然地用箭线图表达他/她对于状态及状态变迁的认知，不要人教都会。跟肌肉记忆类似，像是与生俱来的。反过来看，状态及状态变迁，若不用箭线图表示，还能用什么表示呢？

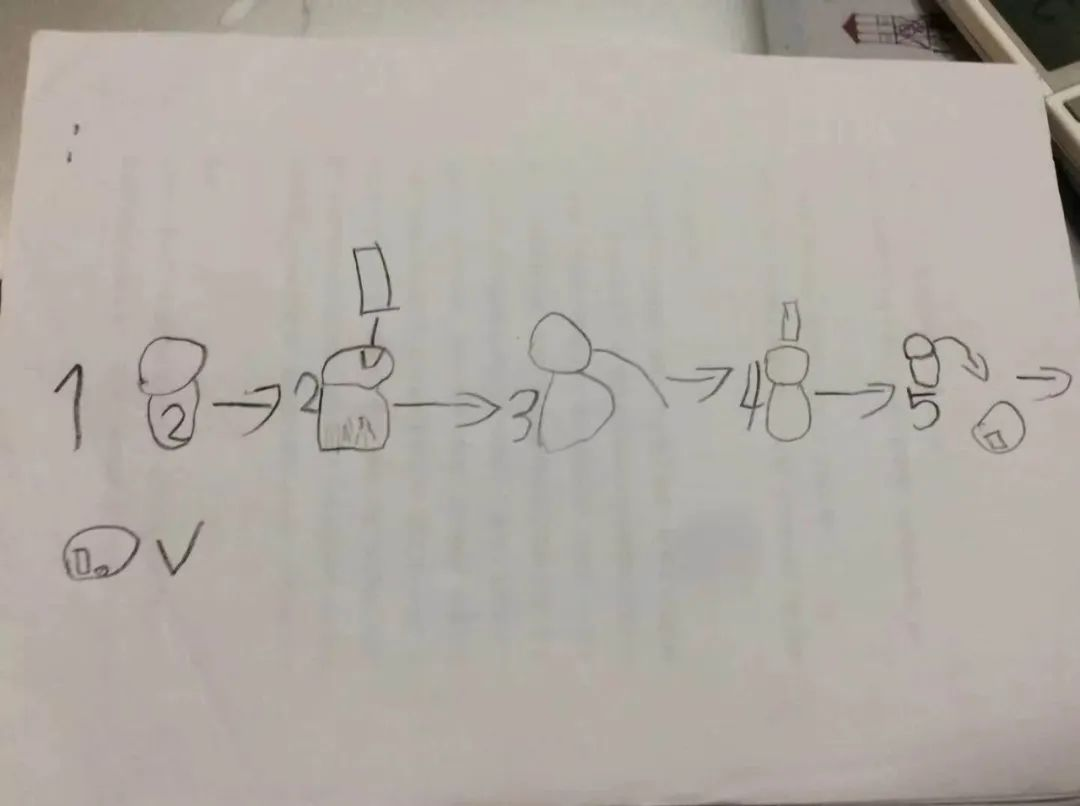
2020年2月12日，六岁多点的小烦（马伯庸）跟妈妈学煮饭。步骤记不住，妈妈让他自己画个图，他就画了下图。他父母也没教过他。

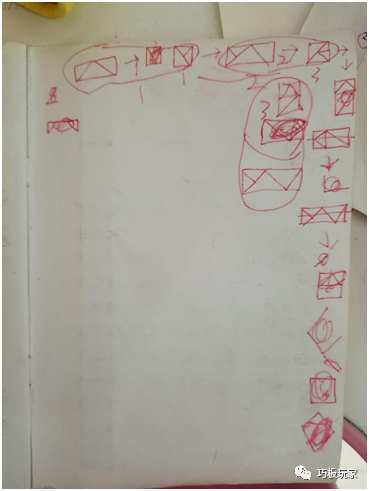
2021年12月10日的七巧板社团课，二年级谢芷菡同学记不住七巧连方的四组变形，她自己画出下图，依图变形。

两个静态的拼图结构之间存在什么样的关系呢？或者说，我们需要什么样的灵活的结构，把静态结构进行动态连接呢？

最普适的，是用箭线图表示。箭尾出发点表示变迁前的状态，箭头射向的点表示变迁后的状态。整个箭线图表示状态及其变迁。

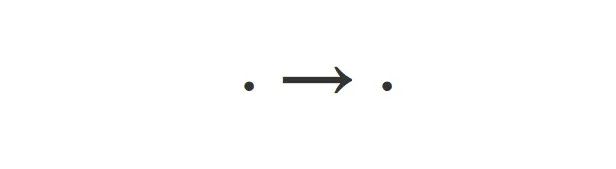
（三）

上文中曾提及：若一个拼块，经过一次翻转变换，从起点出发又回到起点，终点与起点彼此重合彼此相等，我们就说该拼块构成一种翻转对称。

我们可以表示成这样的箭线图：

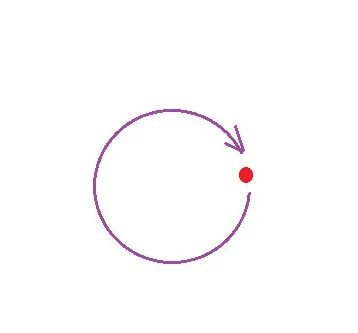
至此，我们来尝试理解下图：

只要孩子们喜欢，把箭线图中的点替换成小猪。上图中的那只小猪既是变换的起点，又是变换的终点，表明它从自身出发，变来变去，又回到自身。上图中，小猪有三种变换都可以变回自身。

基于这种关系图式，我们可以用这种最普适的语言去表达出更多比较复杂的关系：

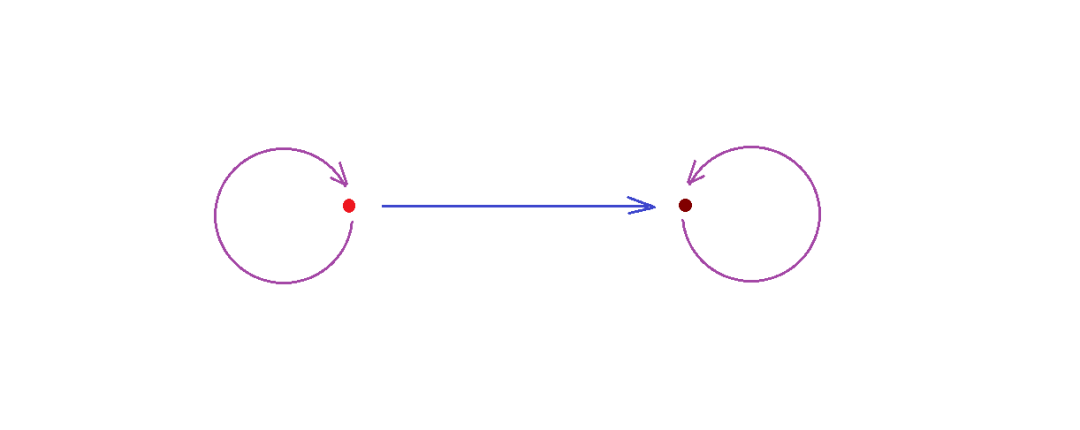
已发文章>>

001 阅读《数学的故事》有感

002 我想和数学谈场恋爱

003 数学“化错”中的美

004 让数学思考成为数学课堂的主旋律

005 卢梭的“错”？

006 数学教学案例《找次品》

007 基于优化学生数学思维的高效课堂创建——以等腰三角形的判定一课为例

008 从特殊到一般，引导数学思维

009 数学文化融入家庭教育的研究

010 sin 震荡函数的图像分析

011 四阶幻方的“太极图”性质

012 无理数的定义和实数理论的建立

013 一个容易被忽视的问题——数学文化

014 “双减”背景下初中数学学科的合作学习方式探究

015 中学数学德育渗透的方法与路径

016 《数学的力量》读后感

017 基于数学文化的单元统整教学设计——以“圆的认识与面积”教学为例

018 有助于数的理解的数字圈环

019 以折叠为例，探究生长型数学教学模式

020 我从事数学科普写作的经验与启示

021 在阅读中滋长智慧——读《教育智慧从哪里来》有感

022 学习数学史 做数学的使者

023 开数学文化之窗 启数学文化魅力——阅读《美丽的数学》有感

024 “文学独白”——数学教学因你而精彩

025 如何用多面体三等分正方体

026 HPM视角下《圆的周长》教学设计

027 被误解的“勾股定理”

028 好玩的数学

029 帮小青蛙设计一个井

030 万物的基础——数学——读《从一到无穷大》有感

031 读《孙子算经》鸡兔同笼问题有感

032 HPM视角下高中数学多样化作业的设计

033 攀越高峰的领路人——数学文化

034 我的好兄弟：数学

035 细嗅数学文化之香

036 藤蔓的喜悦

037 物理力学中数学的影子

038 复数外传

039 函数的历史和发展

040 数学文化与我

041 数学之趣

042 探索数学知识背后的秘密

043 数学文化和我的数学学习

044 古代算数几何形体——阳马与鳖臑

045 数学文化与我的数学学习

046 我与数学文化

047 “形象”的数学

048 站在巨人的肩膀上学习数学

049 从数学文化和个人影响的角度剖析对数的历史

050 论数学文化

051 我与数学文化

052 正弦定理的源起与应用

053 数学文化融入初中数学教学的实践与思考

054 给数字爱好者的1个全新的0至9数字思考挑战及应用问题

056 奇妙的规律

057 生活中的“家常便饭”——数的表示方法

058 读《黄东坡智慧大讲堂——带你发现数学之美》有感

059 通识教育视角下初中数学思维培养从直观向抽象过渡的研究

060 读《古今数学思想》有感

061 为什么圆的面积的导数等于周长？球的的体积的导数等于其表面积？

062 《奇妙的数学文化》读后感

063 数学文化视角下《九宫图的奥秘》教学设计

064 关于毕达哥拉斯定理适用蒙特卡罗方法验证的探讨

065 遨游数学星空，体味数学奇妙

066 核心素养下的，数学文化中的美育渗透

067 探寻数学之奇，欣赏数学之美