和差角公式记忆口诀,高中数学三角函数公式快速记:倍角公式和半角公式轻松掌握有方法
在掌握了三角函数两角和差公式之后,我们可以根据两角和差公式,轻易地掌握三角函数倍角公式和半角公式。
如果还没有掌握两角和差公式,可以先参看相关的内容,待掌握后再进行下面的环节,否则效果不佳。
高中数学三角函数公式轻松记:正弦余弦的两角和差公式“口诀”记
上面是介绍的正弦和余弦的两角和差公式如何熟记,主要是应用口诀“正异同,余同异”快速掌握。
高中数学三角函数公式轻松记:正切余切两角和差公式的推导与记忆
上面是介绍正切和余切的两角和差公式如何推导及快速记忆之法。
在这些熟练掌握后,我们就能很轻易地掌握和运用倍角公式和半角公式了。

三角函数二倍角公式
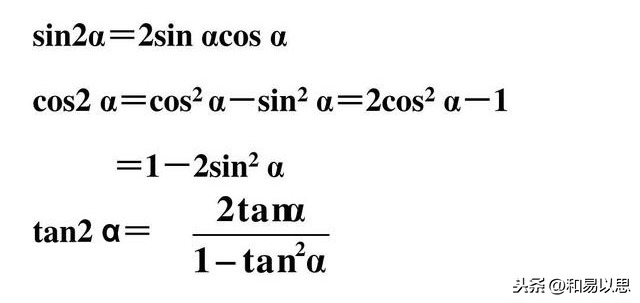
三角函数二倍角公式
在三角函数加法公式(即两角和差公式)中我们学习的是有两个角,其中一个用α表示,另一个用β表示。
当我们现在用来记二倍角公式时,也就是一个角的2倍,而一个角的两倍就是这个角和自己相加的结果。
所以我们把两角和差公式中的两个不同角变为相同的角时,两角和差公式也就成了二倍角公式。
比如sin(α+β)当α=β时,sin(α+β)=sin2α=sin2β,后者不就是二倍角吗?
所以只要掌握了三角函数的两角和差公式,我们把公式中的不同的两个角当作相同的角时就直接可以写出二倍角公式了。
sin2α=sin(α+α)=sinαcosα+cosαsinα=2sinαcosα.
同理可以写出其他形式的三角函数的二倍角公式,大家不妨自己写一下看看。
这里要提示下的是余弦的二倍角公式在写出后,然后利用sinα+cosα=1这个关系式,又可以推导出两个公式。
比如cos2α=cos(α+α)根据口诀“余同异”,可以直接写出余弦的两角和的公式如下:
cos2α=cos(α+α)=cosαcosα-sinαsinα=cos²α-sin²α.①
根据sin²α+cos²α=1,可以分别得出 sin²α=1-cos²α和cos²α=1-sin²α。
分别代入①式就可以得出余弦的二倍角公式的另外两个常用的公式表达式了。
二倍角公式上面是推理来的,如果不推理,也可以利用前面介绍的方法通过观察找特点直接写出公式。
比如sin2α,这是正弦,按照“正异同”知道其公式展开式中的每一项都是相异的同组组成的,所以每一项都是sinαcosα,这样看到正弦可以直接写出此项,然后前面加个2就可以了。(想想为什么)
再看cos2α,根据口诀“余同异”,可以直接写出cos²α-sin²α.
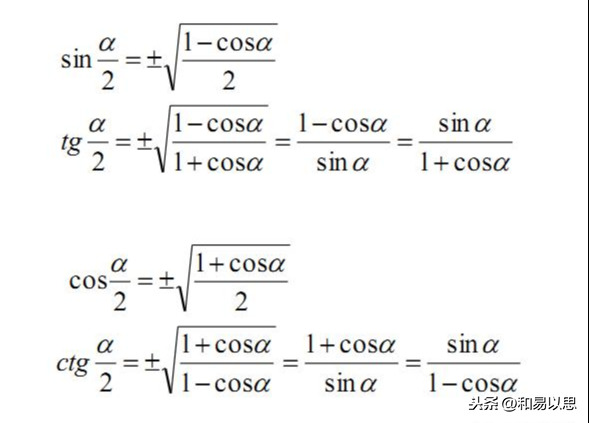
三角函数半角公式
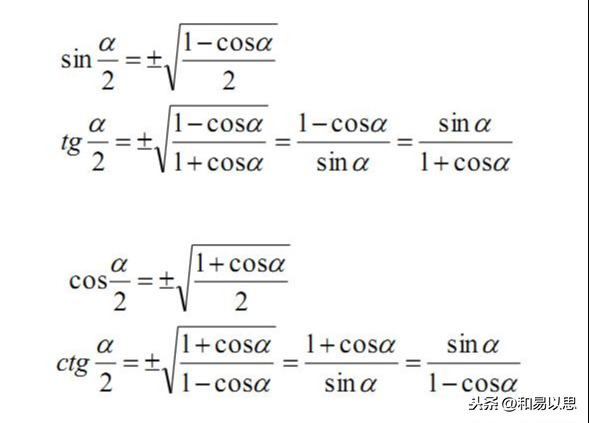
三角函数半角公式
这里的tg也就是tan,是正切;ctg也就是cot,是余切。不过现在教材更多采用的是tan和cot来表示正切和余切。
可能大家一看公式,感觉很复杂,不好记。
其实这些公式都是来自于余弦的两角和差公式。
余弦的两角和差公式,当我们把两个不同的角当作相同的角看待时就变成了余弦的二倍角公式。
其中一个是:cos2α=2cos²α-1 ②
另一个是: cos2α=1-2sin²α ③
为何采用余弦的二倍角公式而不是正弦的二倍角公式?
原因就在于正弦的二倍角公式等式右面不知一个三角函数,而是同组的相异的两个三角函数。
我们现在观察②式,发现等号左边的角是 2α,等号右边的角是 α,有没有发现什么特点?
右面的角是左边的角的一半!
③式也同样如此。
也就是说等式左边的角是右边的2倍,所以是二倍角公式。
从右边的角的角度来看,右边的角是左边的角的一半,岂不就是半角公式吗?
当然根据公式的常用表示法,一般展开式在右边,所以我们需要把半角放在等式的左边。由此有:
②式变换为 2cos²α-1 =cos2α → 2cos²α=1+cos2α → cos²α=(1+cos2α)/2,
然后开方就可以得到公式的形式。(切记:开平方结果有两个,一正一负,具体选择哪个符号,还是取决半角函数的符号)
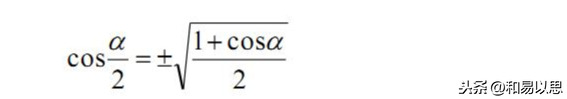
余弦半角公式
为了符合我们一般的习惯,我们不用α表示半角,而是用α/2表示,所以2α也对应变成了α。
所以余弦的二倍角公式,因而变为:
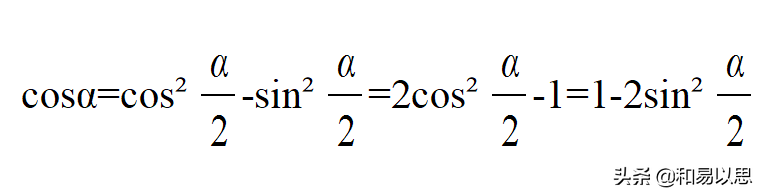
根据这个式子可以得出三角函数的降幂公式,只需要再变化下即可。这个不再展开论述。
这个方法也就是比较等式两边的角的关系,然后由一边的角表示另一边,这样就可以得到不同的公式,不过从根源上看还都是一个公式的变化而已。
如果没有掌握这个特点,很可能会为公式繁多而忧虑,并且还很容易遗忘或记混淆。
思路:余弦的两角和差公式 → 二倍角公式(令两角相等)→ 半角公式(比较等式两边角的关系) → 降幂公式。
如:

三角函数降幂公式
由于这里是介绍公式记忆和方法的,所以不再论述不同公式如何使用以及在具体题目中我们应该如何根据题目条件和要求确定用哪个公式。
正切和余切的半角公式,也是先用正弦除以余弦公式,然后将对应的正弦和余弦的半角公式代入,最后采用分子有理化或分母有理化而分别得到两个去除根式的公式表达形式。(无论是根式中分子或分母中的1+cosα还是1-cosα,都是采用构成1-cosα的形式进行分母或分子有理化的,因为这样就是sinα,可以直接开出来了。这也是平方差公式的逆运用。)
和差角公式记忆口诀,高中数学三角函数公式快速记:倍角公式和半角公式轻松掌握有方法

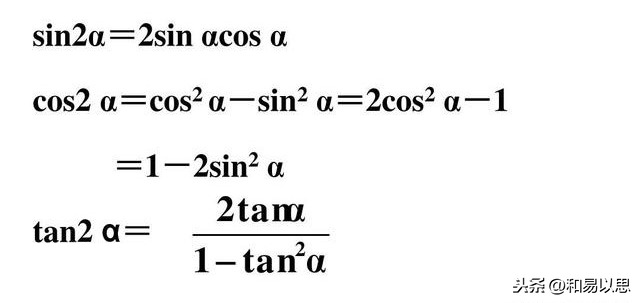
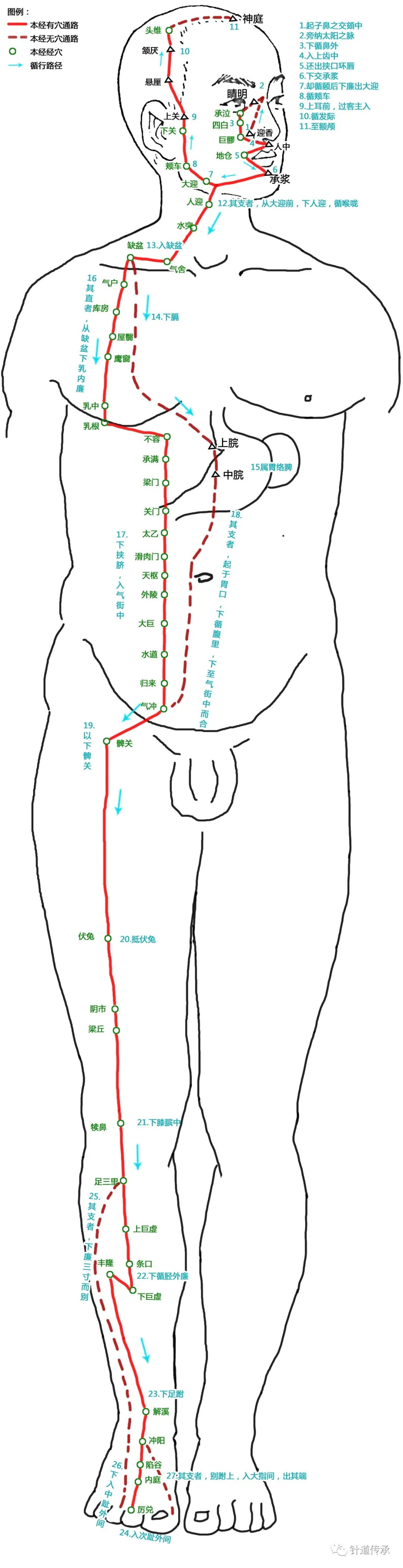
十二经络歌诀记忆法,十二经脉太难记?这篇十二经脉解读汇总全告诉你!附歌诀、高清图
怎么才能记忆力提高,强大的记忆力,究竟是如何炼成的?



高中生如何增强记忆力,高中生学习成绩差?老师给你6个小妙招,助你期末考试拿高分




吃什么补脑增强记忆力,记忆变差?补脑靠7种食物

一个月背3500单词实际吗,70后搬砖妈妈,为儿子英语高考,硬背高考3500单词
精选推荐
- [记忆方法] 最有效的备考方法,法考如何备考,2021年高考备考:8种高效记忆方法
- [记忆方法] 考前快速大量记忆技巧,最有效的备考方法,考前冲刺:一消备考也要动脑筋,这样记忆方法大多数考生并不知道
- [记忆方法] 怎样快速记忆知识点且记得牢,考前快速大量记忆技巧,会计从业备考不放假,六大归纳记忆法带你飞!
- [记忆方法] 快速记忆方法的小窍门,怎样快速记忆知识点且记得牢,这些记忆方法让你学习、备考的效率大大提升!
- [精品记忆课] 记忆课程有没有效果,记忆力课程,“超强记忆”吸引家长买了课,没上几节校长就失联,41名家长能要回16万余元的培训费用吗?
- [精品记忆课] 最强大脑记忆训练法视频,记忆课程有没有效果,超强记忆系统课_第2节 底层逻辑篇 超强记忆系统课_第2节
- [古诗词记忆] 孩子记忆力差,背书困难怎么办,有什么快速背书的方法,有用的背书方法,快收藏码住吧~
- [记忆方法] 记忆的方法和技巧,记忆宫殿训练方法,技巧:熟记这些顺口溜,轻松记忆历史朝代知识
- [记忆方法] 历史朝代记忆口诀,记忆的方法和技巧,我国历史朝代顺序记忆口诀
- [古诗词记忆] 文科怎么背怎样才能记得住,文科背书怎么背得快又牢固,文科成绩难提高?你需要这12个方法