数学系毕业后干什么最挣钱，猜证结合思想之“数学归纳法”在高中数学解题中的应用

一、猜证结合思想概述

解题的核心是逻辑推理，因此我们要着力研究：怎样进行逻辑推理。

在数学上“逻辑”通常是指“思维的规律”，它不仅包括形式逻辑推理，而且包括辩证逻辑推理以及各种非形式化的逻辑推理，如形象思维、直觉思维等等。因此我们要尽力引入运动和辩证的方法，全面而深刻的学会推理。

解题是人类特别富有的智力活动，它必须遵循人类认识运动的规律。

人的基本认识过程有两个：一是由特殊到一般；一是由一般到特殊。我们按照这两个基本认识过程，将推理分为两种：

1、似真推理 —— 由特殊到一般，这种推理也叫做归纳推理，这是创造性的逻辑推理。

“由特殊到特殊”或“由一般到一般”的推理，叫做类比推理。其认识过程仍包含于“由特殊到一般”这个基本认识过程之中，并且所推出的结论也是似真的，所以类比推理也是似真推理。

2、证明推理 —— 由一般到特殊的推理，叫做演绎推理，这是必然性的推理，我们把演绎推理也叫做证明推理。

我们把似真推理和证明推理，简言为“猜想和证明” ， 数学推理总是这样 “猜想——证明——再猜——再证”循环往复的进行的，直到问题解决或发现新问题，这就是数学推理的逻辑，由此凝聚了一个现代的解题思想——猜证结合思想。

二、数学归纳法概述

“数学归纳法”是证明与正整数有关的命题的一种方法，它的理论依据是数学归纳原理：

设 P（n）是关于正整数 n 的一个命题，如果：（1）P（1）真 ；（2）由P（k）为真的假设可推出 P（k +1）也为真，那么 P（n）对一切正整数 n 为真 。

数学归纳法是人们以有限把握无限，通过有限次操作证明无限集合的命题。它第一次提供了证明无限集合的命题的一种确切而严谨的教学方法，这个方法是完全归纳法。

数学归纳法证明命题 P（n）（n ∈ N, 且 n ≥ n0）成立的一般步骤

（1）证明 P（n0）成立 ；

（2）假设 P（k）（k ∈ N, 且 k ≥ n0）成立 ，证明 P（k + 1）也成立 。

根据 （1）和 （2），可知 P（n）对一切正整数 n （n ≥ n0）都成立 。

例题：求证：

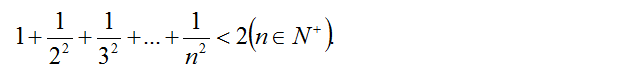
例题图（1）

猜证：这是 P（n）命题，用数学归纳法证明 。

第一步：当 n = 1 时 ， 1 < 2 显然成立 ；

第二步：假设 当 n = k 时 （k > 1）

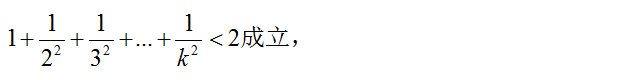
例题图（2）

则 当 n = k + 1 时 ，

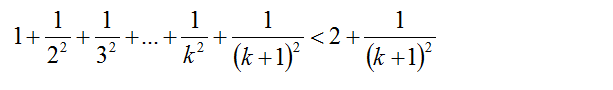
例题图（3）

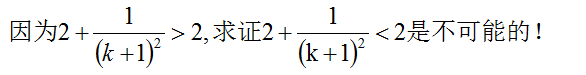
例题图（4）

因此数学归纳法失效！若还想用数学归纳法证明，就得变换命题，使不等式的右边与 n 有关 。

经过几次试验猜想，改证如下：

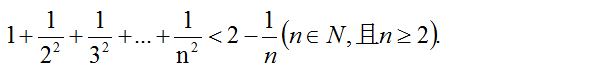
辅助不等式图（5）

证法一：先用数学归纳法证明上图中的辅助不等式：

（1）当 n = 2 时 ， 左边 = 1 + 1/（2^2）= 5/4 ，右边 = 2 - （1/2）= 3/2 ，

所以左边 < 右边 ， 上图中的辅助不等式成立 。

（2）假设 n = k （k ≥ 2）时

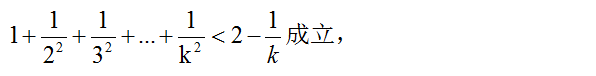
例题图（6）

则 当 n = k + 1 时

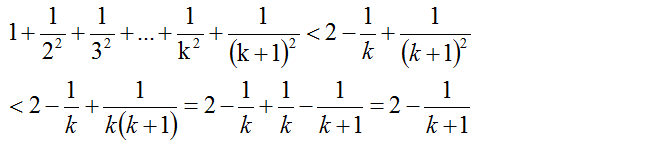
例题图（7）

即上图中的辅助不等式也成立。

由 （1）和 （2），可知上图中的辅助不等式成立 。

又因为 2 - 1/n < 2 , 且 当 n = 1 时原不等式为 1 < 2 显然成立，所以

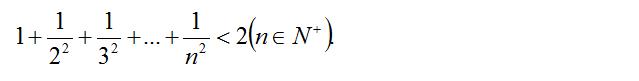
例题图（8）

得证 。

注：P（n）命题不一定都必须用数学归纳法证明，给出证法二——列项相消放缩法！

证法二、列项相消放缩法

例题图（9）

注：（1）当数学归纳法失效时，可引进辅助命题，再用数学归纳法；

（2）本题不宜使用数学归纳法，用列项法最为简捷。

解题时注意依据问题的特点，选择最快最好的方法。

欢迎关注头条号“尚老师数学”！