「译者 | 实验室的猫」语：数学是一门神奇而美丽的学科，不仅只是公式、数字和计算的堆砌，更是一种思维方式，一种独特的观察世界的方式。

下面文章译自Kevin Houston公开提供的《10 Ways To Think Like A Mathematician》一书的试读小册子，这篇简短介绍展示了如何像一位数学家那样思考，如何用数学的眼光看待问题，以及如何运用数学的思维方法思考的难题。(这本书似乎暂时还没有中文版)

让我们首先承认一个事实：学数学确实不容易。然而，我坚信——而且信念坚定——只要你能像数学家那样洞察问题，学习数学的过程就会变得更加轻松。

因此，我的使命就是引导每一位学生，如何从数学家的角度去洞察世界。

这本小册子，正如它的标题所述，给出了十种方法，让你更接近数学家的思维方式。实际上，这本小册子是我畅销书籍《如何像数学家一样思考》的试读版。如果你希望避免单纯的应试学习，渴望真正理解数学的精髓，那么这本书就是为你而写的。

我希望这本小册子能激发你的灵感。如果有的话，请告诉我。我很想听听你的想法。

1. 质疑一切

在我看来，数学的魅力在于其能够被验证。你无需盲目接受别人的观点。如果有人宣称某事是真的，你完全可以要求他们来证明它。

更进一步，如果你真的希望像数学家那样思考，甚至可以自己去尝试把它证出来。不要让别人喂饭给你！

你应该对他人的陈述持有怀疑的态度，试图找到反例来证明他们的错误。即便对方的观点是正确的，通过此种方式锻炼出的思维方式也是有益的。这种方式也有助于培养对于命题的敏感度。

比如，有人声称，从逻辑的角度思考，时间旅行是不可能的：如果时间旅行可能，那么我们自然会遇到很多来自未来的人。

对此，我能找到一些反驳的观点。比如，时间旅行只允许人向未来移动时间；时间旅行者不被允许与我们交流；时间旅行有一个范围，你不能回溯超过一年，而时间旅行还需要很多年才能实现（而且时间机器并不能被随时光运输）。

2. 写好每一句话

写好每一句话？你可能会问，这怎么会帮我像数学家一样思考？其实，一句完整准确的句子是论证的基础，高级数学更是关于证明的艺术，而不仅仅是得到正确的数值答案。

然而，许多学生忽视了书写句子的重要性。他们可能会抱怨：“我来上大学不是为了写论文的！”、“但我的答案是正确的！”或者“你知道我想说什么的！”

但是，如果你想真正理解数学并清晰地思考，你需要遵循句子书写的规范，这会让你非常仔细地思考你所论证的内容。如果你不能把句子正确地写出来，那么可能真的不清楚正在写什么。

这也是一个学习更多并提升你的技能的好机会。无论在哪个主题上，良好的写作都是一项有用的技能。因此，当你在写数学论证时，不要忽视句子的重要性。通过书写精确、清晰的句子，将更好地表达自己的想法，更好地理解数学，也更能成为像数学家一样思考的人。

【附加内容】提高你的数学写作和思维的一种简单方法是要知道如何正确使用 ⇒ 蕴含符号。详见《如何像数学家一样思考》第 37-38 页和第二部分。】

3. 逆命题的奥秘是什么？

形如 A ⇒ B 的命题是数学的核心。我们也可以说“如果 A 为真，那么 B 就为真。而对于这样的命题，我们还有一个亲密的伙伴，那就是它的逆命题，写作“B ⇒ A”。

• 例如，“如果我是温斯顿·丘吉尔，那么我就是英国人”的反命题是“如果我是英国人，那么我就是温斯顿·丘吉尔”。

”这个例子生动地揭示了一个事实：即使一个命题为真，它的反命题并不一定为真。反命题可能真，也可能假。我们需要通过深入的研究才能得出明确的结论。

作为一名优秀的数学家，当遇到一个“如果 A，则 B”类型的命题时，会自然而然地提出：“那它的逆命题成立吗？”这个问题应当深深地烙印在你的数学思维中，成为你的数学工具箱中重要的一部分。

实际上，无论逆命题是否为真并不重要，真正重要的是这个过程能助力你的数学思维变得更为敏锐。顺便提一句，人们在处理"A ⇒ B"时常犯的一个大错误是，他们认为如果 A 不为真，那么 B 也不为真。这是错误的，该命题只阐述了当 A 为真时会发生什么，而并未涉及到当 A 为假时的情况。那么，让我们一起挑战一下，像数学家一样思考，自己找出一个例子吧！

4. 探索逆否命题的奥秘

逆否命题(contrapositive)是陈述式 'A ⇒ B' 的对应形式, 即 ¬B ⇒ ¬A。

例如：

• '如果我是温斯顿·丘吉尔，那么我就是英国人' 的逆否命题是 '如果我不是英国人，那么我就不是温斯顿·丘吉尔'。

• '我不是美国人，因此我不是德克萨斯人' 的逆否命题是 '如果我是德克萨斯人，那么我是美国人'。

• 'x^2 - 4x -5 =0 ⇒ x \geq -2' 的逆否命题是 'x < -2 ⇒ x^2 -4x - 5 ≠ 0'。

令人惊讶的是，逆命题的真值与 A ⇒ B 的真值相同！也就是说，如果 A ⇒ B 为真，那么 ¬(B) ⇒ ¬(A) 也为真，反之亦然。

以上例子就为这一点提供了验证。这个概念初接触时可能难以理解，不少人都会有所质疑。实际上，有一个知名的教育实验与逆否命题的概念紧密相关，被称为华生选择任务(Wason’s selection task)。你是否愿意去试一试看能否通过这个测试呢？通过的人不足 10%。由于逆否命题在证明中的广泛应用，以及我们在日常推理中对逆否命题的常见误解，因此你应该好好地研究和理解它。

5. 考虑极端情况

在研究数学定理时，我们应该尝试将其应用于一些平凡的(trivial)或极端的值例子。例如，可以考虑将特定的数字取为 0 或 1，或者使用由 f(x)=0 定义的平凡函数，采用空集或平凡序列如 1,1,1,1,1...，或者考虑使用圆或直线等特殊情况。这些实例有助于我们更深入地理解定理，并能更清晰地揭示定理适用的情况。这种方法被称为“考虑极端的情况”。

[实验室的猫]：在数学中，“trivial”通常翻译为“平凡的”或“显然的” ，将费马大定理描述为方程 aⁿ+bⁿ=cⁿ 对 n > 2 没有非平凡解。 显然，这个方程确实有解。比如 a=b=c=0 对任何 n 都是解，a = 1, b = 0, c = 1 也一样。但是这种解是显然而无趣的，从而称为平凡。

这些实例有助于我们更深入地理解定理，并能更清晰地揭示定理适用的情况。

举个例子，考虑这样的陈述：“y=x²,z=y²，因此 z≠x²”。这个推理看上去似乎合情合理，因为 y 和 y² 通常是不同的，但实际上这并不正确。试想当 y=x=1 的情况下， z 是等于 x² 的。这个例子清晰地展示了考虑极端例子的重要性，这种方法有助于我们更好地理解和运用数学定理。

另一个例子是考虑这个命题：“假设 a,b,c 和 d 是整数。如果 ab=cd 且 a=c，则 b=d”。要证明这个命题是错误的，我们可以采用极端例子的方法。为此，我们需要积累足够的例子并熟练掌握它们。假设 a=c=0，那么我们可以选择 b=2 和 d=1，这样就满足了条件 ab=cd，但 b ≠ d，从而推翻了这个错误的命题。

总之，考虑极端例子是一种有用的方法，它能够帮助我们更好地理解和应用数学定理。在数学研究中，可能会遇到需要快速想出例子的情况，因此我们需要积累足够的例子并熟练掌握它们，以便在需要时能够迅速套用。

6. 构建你自己的例子

真正的数学家会设计出他们自己的例子，无论是标准的、极端的、还是反例！

让我们来看个较熟悉的例子，来体会整个流程吧。假设正在微积分的世界里探索函数的极大值和极小值。

首先需要理解函数是如何求导。然后，我们会了解到，那些导数值为零的点就是所说的驻点。接下来，会发现奇异点有三种形式：极大值、极小值和拐点。而函数的二阶导数能够帮我们确定这些驻点的类型。然后，我们就能看到一个具体的例子：这是一个函数，这是它的驻点，这是驻点的类型。这个过程看似简单，给定函数 f，对 f 求导，然后求解 f'(x) = 0，再次求导得到 f"(x)，并且通过 f"(x) 的正负号判断驻点的类型。

这就是标准的处理方法。掌握了这个步骤，你就能轻松找出给定函数的极大值和极小值。然而，如果我换个角度问你：能否构造一个函数 f，使其在 x=2 处达到最大值，在 x=-6 处达到最小值？这无疑是对你理解程度的更大考验，难度也更大。然而，正是在挑战这样的问题过程中，你能深入理解数学的魅力。

因此，面对已解答的例子，你应当逆向思考，自创新问题。更有趣的是，你可以与朋友们共同创造这些问题，交换彼此的问题，从而获取更多的练习机会。你甚至可以组织一场竞赛，看谁能设计出最具挑战性，但又能解决的问题。

7. 假设在何处发挥作用？

我经常听到学生们说，他们觉得理解数学证明非常困难。实际上，这并不出乎意料，因为证明往往是出于逻辑和效率的考虑，而非为了提供对定理表述的深度理解，或者揭示如何发现证明的过程。学生们常常陷入困境，甚至无法独立下手。

是的，理解证明的过程，无疑是迈向数学家之路最艰难的部分之一。《如何像数学家一样思考》的第 18 章全篇都是关于理解证明的各种策略——例如，分解证明，将证明应用于实例。我们只需考虑下面的技巧。

每个定理都有其假设。比如，毕达哥拉斯定理就会先假设平面上有一个直角三角形。这些假设在证明中必然会被使用，否则就成了无用之物。因此，积极寻找假设在何处被使用，你就能开始理解证明的过程。

有些假设可能不会直接阐明清楚。比如，证明可能会说“……根据定理 5.7，我们发现……”，而定理 5.7 可能需要更前面的某个假设。（顺便一提，如果一个定理在不同的证明中被反复使用，那它一定具有重要性，可能会被用在你的证明中，所以务必深入学习理解它。）

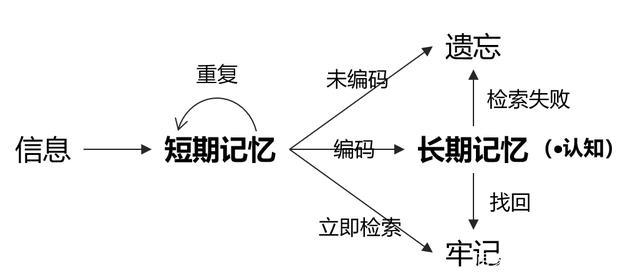
通过搞清假设，你就能开始步入证明的世界，学习其结构和内在联系。作为额外的奖赏，你的记忆也会得到加强，因为不再是被动接受信息，而是在主动探求知识。这种主动探求的过程，无疑能让你更好地理解和记住所学的内容！

8. 从复杂的一方开始

我最重要的一条建议是：在证明等价性时，通常最好从等式较为复杂的一方开始，逐步替换以简化其复杂性。这样不仅能使问题更加清晰，还能让我们更加明确目标。

例如，为了证明对所有的 x ∈ R（x ≠ nπ/2，n ∈ Z）有 tan x + cot x = 2cosec 2x，我们执行以下步骤：

注意，复杂的一方（或者更准确地说，我们可以进行替代和简化的一方）始终在等式的一边。如果你从等式开始并尝试重新排列它（如许多人所做），那么你有可能陷入循环。你也可能冒着假设必须证明的风险。

9. 提问"如果...会怎样？"

优秀的数学家善于提出这样的诘问：“假设……会怎样？”例如，若我们删掉某项假设，会有何影响？深度探求此类问题，我们能对为何某一结果为真，或者某条定义为何这样阐述，有更深一层的理解。有时候，减弱假设的力度，竟会带领我们走向新的定理的发现！

再举一个“假设”的例子，数学对象通常是在附加某些条件的前提下的集合。在最简单的层次上，我们可以将有限集定义为元素数量有限的集合，但也有更为复杂的例子，如群。（群是一种拥有特定"乘法"运算的集合，且这种乘法需要满足特定的性质。）

现在，假设我们有集合 A 和 B，我们可以构造它们的乘积 A × B。我们可以问：如果 A 和 B 各自具备某种性质，那么 A × B 是否也拥有同样的性质？例如，假设 A 和 B 都是有限集，那么 A × B 是有限集吗？答案是肯定的。如果 A 和 B 都是无穷集，那么 A × B 是无穷集吗？如果 A 和 B 分别是群，那么 A × B 是群吗？如果拓扑空间 A 和 B 是紧致空间，那么 A × B 也是吗？等等。

这个理念在于，我们总是通过提问，去扩展知识边界，加深我们的理解。

10. 交流沟通，知识的交融！

当克里斯托弗·泽曼爵士创立沃里克大学的数学研究所时，他提出的一个核心理念是：为了营造浓厚的数学气氛，研究所应当在走廊里摆放足够多的黑板，而不仅仅是在讲堂内，以便于人们随时停下脚步，互相交流和解释各自的研究。

这种做法不仅可以鼓励合作，更重要的是，它可以让每个人的工作得到他人的检验。剑桥的艾萨克·牛顿研究所更是将这种理念发扬光大，在厕所、甚至在只运行两层的电梯里都设置了黑板！

与他人进行交流沟通有着无数的好处。解释你的工作会促使你更深入、更清晰地思考。你可以从别人那里学习，他们可以指出思维中的漏洞，或者提出解决问题的新思路。甚至你在解说的过程中，也可能获得新的启发。

因此，寻找一个可以交谈的人。没有找到？那就去寻找。如果在教师，试着坐到某人旁边，询问他们如何完成练习 3.2 或者其他的。就从这里开始你的数学之旅吧……