第二数学归纳法怎么理解,第二数学归纳法定义,高三数学知识点-极限
1. ⑴第一数学归纳法:①证明当n第一个n0时结论正确;②假设当n=k(k∈N+,k≥n0)时,结论正确,证明当n=k+1时,结论成立.
⑵第二数学归纳法:设P(n)是一个与正整数n有关的命题,如果
①当n=n0(n0∈N+)时,P(n)成立;
②假设当n≤k(k∈N+,k≥n0)时,P(n)成立,推得n=k+1时,P(n)也成立.
那么,根据①②对一切自然数n≥n0时,P(n)都成立.
2. ⑴数列极限的表示方法:
①
②当n→∞时,an→a.
⑵几个常用极限:
①
(C为常数)
②
③对于任意实常数,
当|a|<1时,
当|a|=1时,若a = 1,则
;若a=-1,则
不存在
当|a|>1时,
不存在
⑶数列极限的四则运算法则:
如果
,那么
①
②
③
特别地,如果C是常数,那么
⑷数列极限的应用:
求无穷数列的各项和,特别地,当|q|<1时,无穷等比数列的各项和为S=a₁/(1-q)(|q|<1).
(化循环小数为分数方法同上式)
注:并不是每一个无穷数列都有极限.
3. 函数极限;
⑴当自变量x无限趋近于常数x0但不等于x0)时,如果函数F(x)无限趋进于一个常数a,就是说当x趋近于x0,函数F(x)的极限为a.记作
或当x→x0时,F(x)→a.
注:当x→x0时,F(x)是否存在极限与F(x)在x0处是否定义无关,因为x→x0并不要求x=x0(当然,F(x)在x0是否有定义也与F(x)在x0是否存在极限无关=>函数F(x)在x0有定义是
存在的既不充分又不必要条件.)
如
在x=1处无定义,但
存在,因为在x=1处左右极限均等于零.
⑵函数极限的四则运算法则:
如果
,那么
①
②
③
特别地,如果C是常数,那么
注:①各个函数的极限都应存在.
②四则运算法则可推广到任意有限个极限的情况,但不能推广到无限个情况.
⑶几个常用极限:
4. 函数的连续性:
⑴如果函数f(x),g(x)在某一点x=x0连续,那么函数f(x)±g(x),f(x)·g(x),f(x)/g(x)(g(x)≠0)在点x=x0处都连续。
⑵函数f(x)在点x=x0处连续必须满足三个条件:
①函数f(x)在点x=x0处有定义;
②
存在;
③函数f(x)在点x=x0处的极限值等于该点的函数值,即
⑶函数f(x)在点x=x0处不连续(间断)的判定:
如果函数f(x)在点x=x0有下列三种情况之一时,则称x0为函数f(x)的不连续点.
①f(x)在点x=x0处没有定义,即f(x0)不存在;
②
不存在;
③
存在,但
5. 零点定理,介值定理,夹逼定理:
⑴零点定理:设函数f(x)在闭区间[a,b]上连续,且f(a)·f(b)<0.那么在开区间(a,b)内至少有函数f(x)的一个零点,即至少有一点ζ(a<ζ<b)使f(ζ)=0.
⑵介值定理:设函数f(x)在闭区间[a,b]上连续,且在这区间的端点取不同函数值,f(a)=A,f(b)=B,那么对于A,B之间任意的一个数C,在开区间(a,b)内至少有一点ζ,使得f(ζ)=C(a<ζ<b).
⑶夹逼定理:设当0<|x-x0|<σ时,有g(x)≤f(x)≤h(x),且
,则必有
注:|x-x0|:表示以x0为的极限,则|x-x0|就无限趋近于零.(ζ为最小整数)
6. 几个常用极限:
更多精彩:「链接」
第二数学归纳法原理,高中数学竞赛有哪些值得推荐的辅导书?数竞党必读!



数学归纳法在哪本书上,高等教育出版社8月22日推出“高中大学数学衔接课”系列公益活动
数学系毕业后干什么最挣钱,猜证结合思想之“数学归纳法”在高中数学解题中的应用

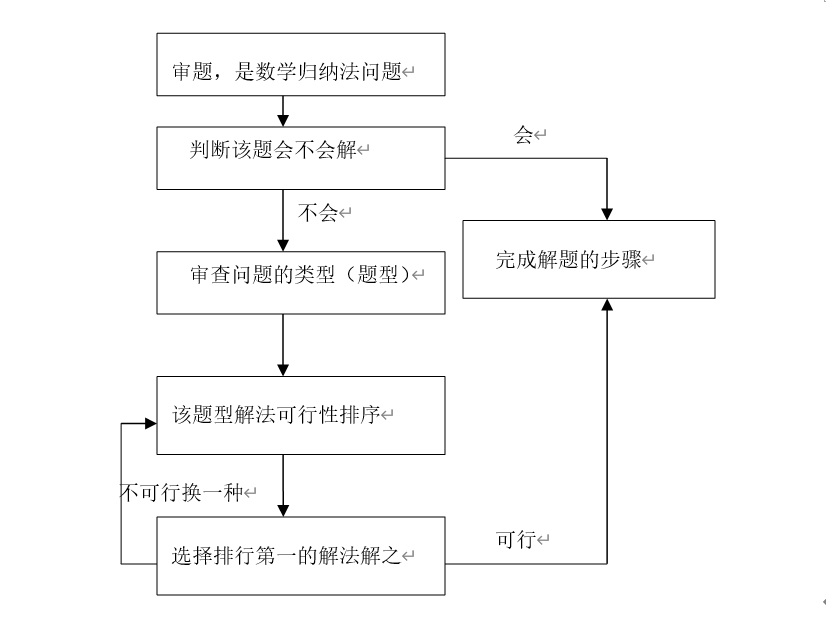
第一和第二数学归纳法,清晰严密的解题思路网络是如何形成的-数学归纳法

第二数学归纳法简单例题,数学归纳法的诞生
精选推荐
- [记忆方法] 最有效的备考方法,法考如何备考,2021年高考备考:8种高效记忆方法
- [记忆方法] 考前快速大量记忆技巧,最有效的备考方法,考前冲刺:一消备考也要动脑筋,这样记忆方法大多数考生并不知道
- [记忆方法] 怎样快速记忆知识点且记得牢,考前快速大量记忆技巧,会计从业备考不放假,六大归纳记忆法带你飞!
- [记忆方法] 快速记忆方法的小窍门,怎样快速记忆知识点且记得牢,这些记忆方法让你学习、备考的效率大大提升!
- [精品记忆课] 记忆课程有没有效果,记忆力课程,“超强记忆”吸引家长买了课,没上几节校长就失联,41名家长能要回16万余元的培训费用吗?
- [精品记忆课] 最强大脑记忆训练法视频,记忆课程有没有效果,超强记忆系统课_第2节 底层逻辑篇 超强记忆系统课_第2节
- [古诗词记忆] 孩子记忆力差,背书困难怎么办,有什么快速背书的方法,有用的背书方法,快收藏码住吧~
- [记忆方法] 记忆的方法和技巧,记忆宫殿训练方法,技巧:熟记这些顺口溜,轻松记忆历史朝代知识
- [记忆方法] 历史朝代记忆口诀,记忆的方法和技巧,我国历史朝代顺序记忆口诀
- [古诗词记忆] 文科怎么背怎样才能记得住,文科背书怎么背得快又牢固,文科成绩难提高?你需要这12个方法