第二种数学归纳法证明,第二数学归纳法什么时候用,斐波那契数列题答案 & 数学归纳法
上一篇文章:宇宙终极奥秘的神秘数列——斐波那契数列 最后的思考题:
斐波那契数列的第100项 与 前98项之和的差是多少?
斐波那契数列:1、1、2、3、5、8、13、21、34、55、89、144……
数列中的每一项称为斐波那契数,从第3项开始,每1项都等于前两项之和。
在数学上,斐波那契数列以如下被以递推的方法定义:
F(1)=1,
F(2)=1,
F(n)=F(n - 1)+F(n - 2)(n ≥ 3,n ∈ N*)
我们知道:
以上,我们发现:
那么,思考计算一下,可变成 第几项 与前1项之和的差?
我们通过观察可以发现:
第n+2项 与 前n项之和 的差 = 第3项 与 前1项之和的差 = 第3项-第1项=第2项
那我们可以用什么方法证明这个等式?
数学归纳法
数学归纳法是以一种不同的方式来证明任意一个给定的情形都是正确的(第一个,第二个,第三个,一直下去概不例外)的数学定理。
虽然数学归纳法名字中有“归纳”,但是数学归纳法并非不严谨的归纳推理法,它属于完全严谨的演绎推理法。事实上,所有数学证明都是演绎法。
数学归纳法原理
最简单和常见的数学归纳法是证明当n等于任意一个自然数时某命题成立。
证明分下面两步:
1、证明当n= 1时命题成立。
2、假设n=m时命题成立,那么可以推导出在n=m+1时命题也成立。(m代表任意自然数)
怎样做
第一步通常是容易的,我们只需证明命题(我们要证明的东西)在 n=1 时成立
第二步最好这样做:
假设当n=k时命题成立
证明当n=k+1时命题成立(以当n=k时命题成立为事实。)
第二步常要用到高明的诀窍!
例如:
例子:3n−1 是 2 的倍数
这是真的吗?我们来看看。
一、 证明当 n=1 时命题成立
31−1 = 3−1 = 2
对了,2 是 2 的倍数。易如反掌。
31−1 成立!
二、. 假设在 n=k 时也成立
3k−1 成立
(慢着!我们怎么知道这是真的?
对,我们不知道!这是个假设。。。。。。接下来,在这例子里我们以此为事实)
现在来证明 3k+1−1 是 2 的倍数
3k+1 也是 3×3k
把 3× 拆开为 2× 和 1×
每项都是 2 的倍数
因为:
2×3k 是 2 的倍数(乘以 2)
3k−1 也是 2 的倍数 (这是我们的假设)
所以:
命题:3k+1−1 是 2 的倍数 —— 成立!
大功告成!
你看到我们怎样利用 "当3k−1 时命题成立"为假设?
我们假设(暂时)"n=k"的成立(当3k−1时命题成立),然后看看这能否让 "n=k+1" 的也成立。
再看一个例子:
做一做:
证明:
第n+2项 与 前n项之和 的差 = 第3项与 前1项之和 的差
第二数学归纳法原理,高中数学竞赛有哪些值得推荐的辅导书?数竞党必读!



数学归纳法在哪本书上,高等教育出版社8月22日推出“高中大学数学衔接课”系列公益活动
数学系毕业后干什么最挣钱,猜证结合思想之“数学归纳法”在高中数学解题中的应用

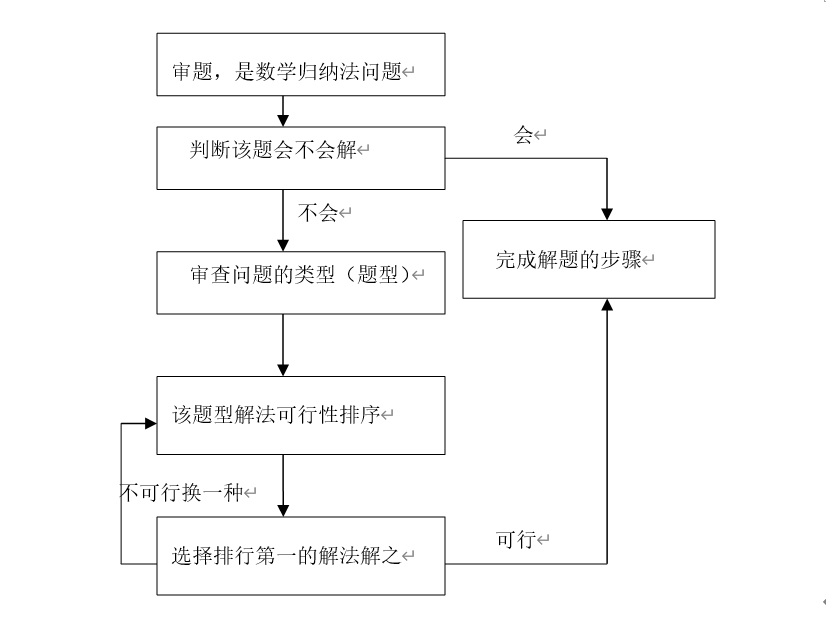
第一和第二数学归纳法,清晰严密的解题思路网络是如何形成的-数学归纳法

第二数学归纳法简单例题,数学归纳法的诞生
精选推荐
- [记忆方法] 最有效的备考方法,法考如何备考,2021年高考备考:8种高效记忆方法
- [记忆方法] 考前快速大量记忆技巧,最有效的备考方法,考前冲刺:一消备考也要动脑筋,这样记忆方法大多数考生并不知道
- [记忆方法] 怎样快速记忆知识点且记得牢,考前快速大量记忆技巧,会计从业备考不放假,六大归纳记忆法带你飞!
- [记忆方法] 快速记忆方法的小窍门,怎样快速记忆知识点且记得牢,这些记忆方法让你学习、备考的效率大大提升!
- [精品记忆课] 记忆课程有没有效果,记忆力课程,“超强记忆”吸引家长买了课,没上几节校长就失联,41名家长能要回16万余元的培训费用吗?
- [精品记忆课] 最强大脑记忆训练法视频,记忆课程有没有效果,超强记忆系统课_第2节 底层逻辑篇 超强记忆系统课_第2节
- [古诗词记忆] 孩子记忆力差,背书困难怎么办,有什么快速背书的方法,有用的背书方法,快收藏码住吧~
- [记忆方法] 记忆的方法和技巧,记忆宫殿训练方法,技巧:熟记这些顺口溜,轻松记忆历史朝代知识
- [记忆方法] 历史朝代记忆口诀,记忆的方法和技巧,我国历史朝代顺序记忆口诀
- [古诗词记忆] 文科怎么背怎样才能记得住,文科背书怎么背得快又牢固,文科成绩难提高?你需要这12个方法